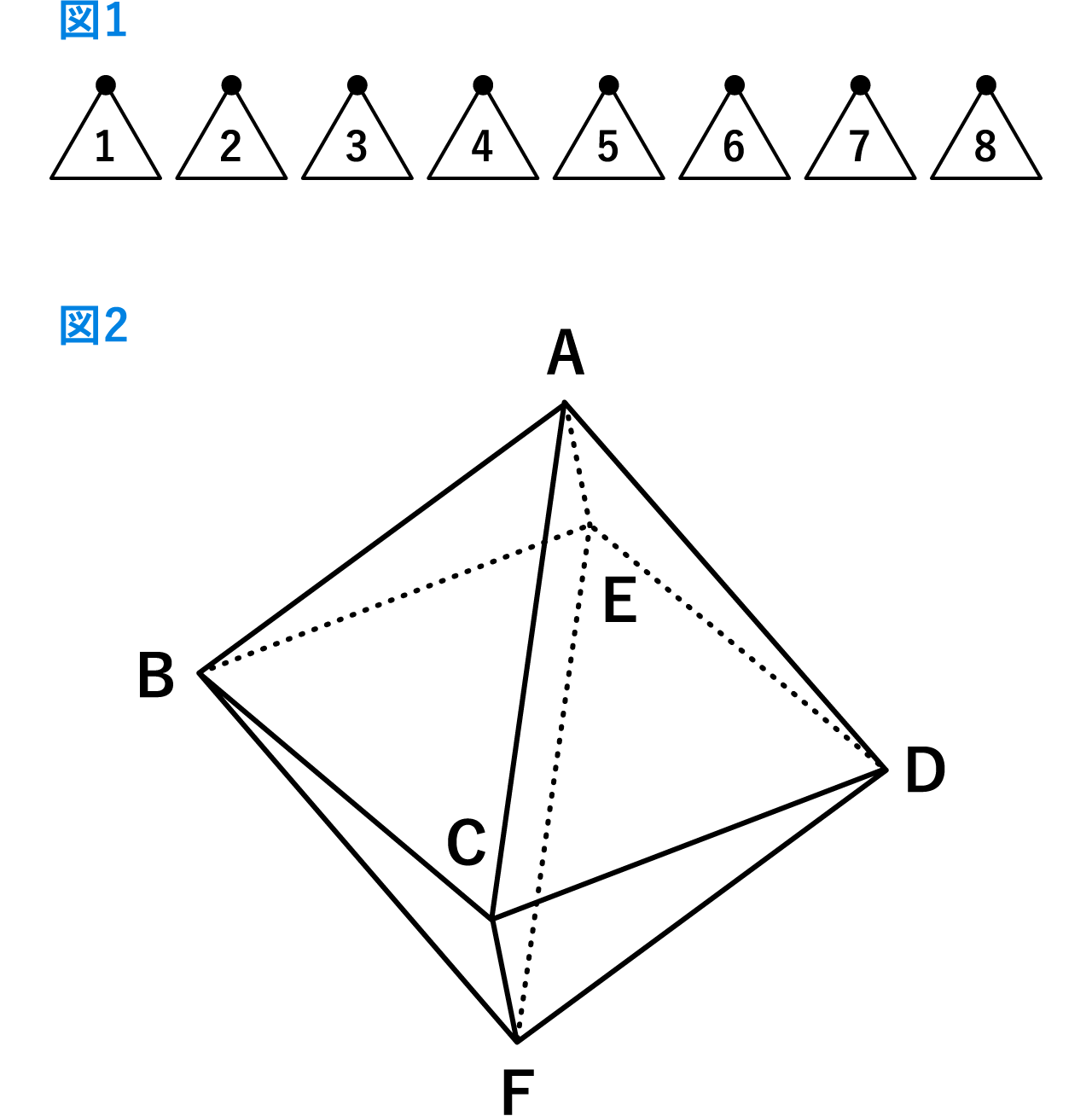
図１のように１から８までの数字が書かれている８枚の正三角形を用いて、
図２のような立体を作ります。
ただし、図１の正三角形の黒丸の頂点は立体の点Ａまたは点Ｆのどちらかに重ね、
すべての数字が表から見えるようにします。

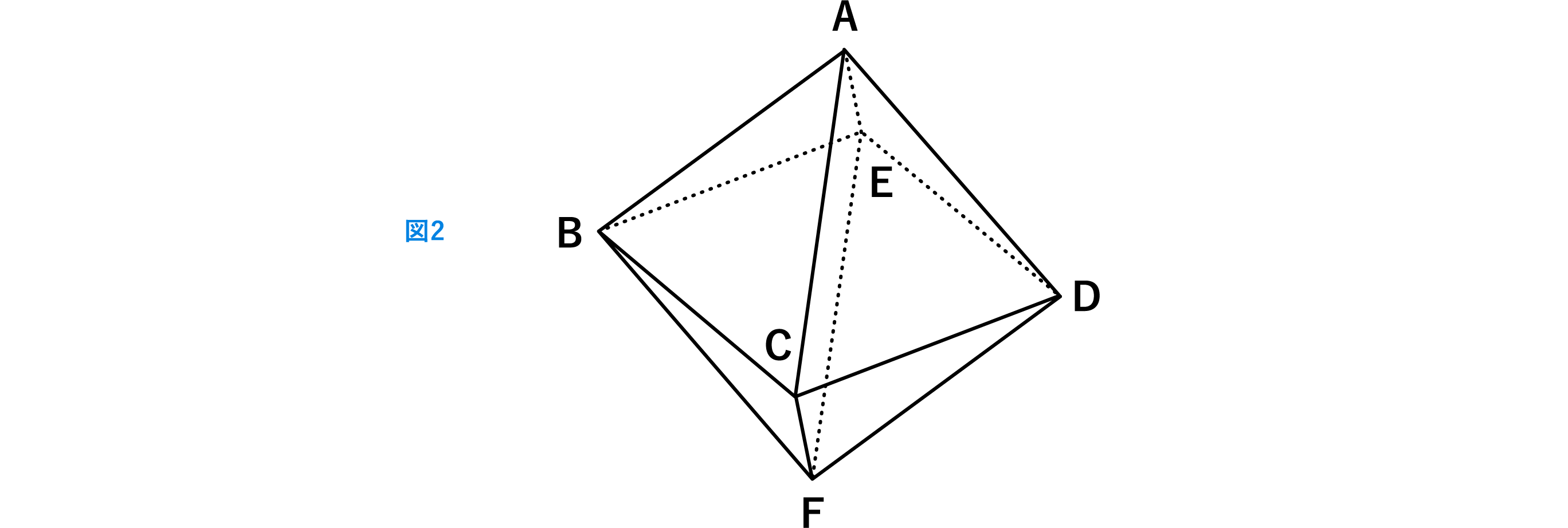
また、立体の６個の頂点Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆについて、
それぞれの頂点に集まっている４枚の正三角形に書かれている数の合計はすべて同じになっています｡

（１）1つの頂点に集まっている４枚の正三角形に書かれている数の合計を求めなさい。

（２）辺ＢＣを１辺とする２枚の正三角形に書かれている数の合割と、辺DEを１辺とする２枚の正三角形に書かれている数の合計は等しくなります。その理由が書かれた次の文章の（空欄）をうめなさい。

「どちらも（　　　　　　　　）すると、同じ値になるから」

（３）三角形ABCに書かれている数が１であるとします。
８が書かれている三角形として可能性があるものをすべて選びなさい。

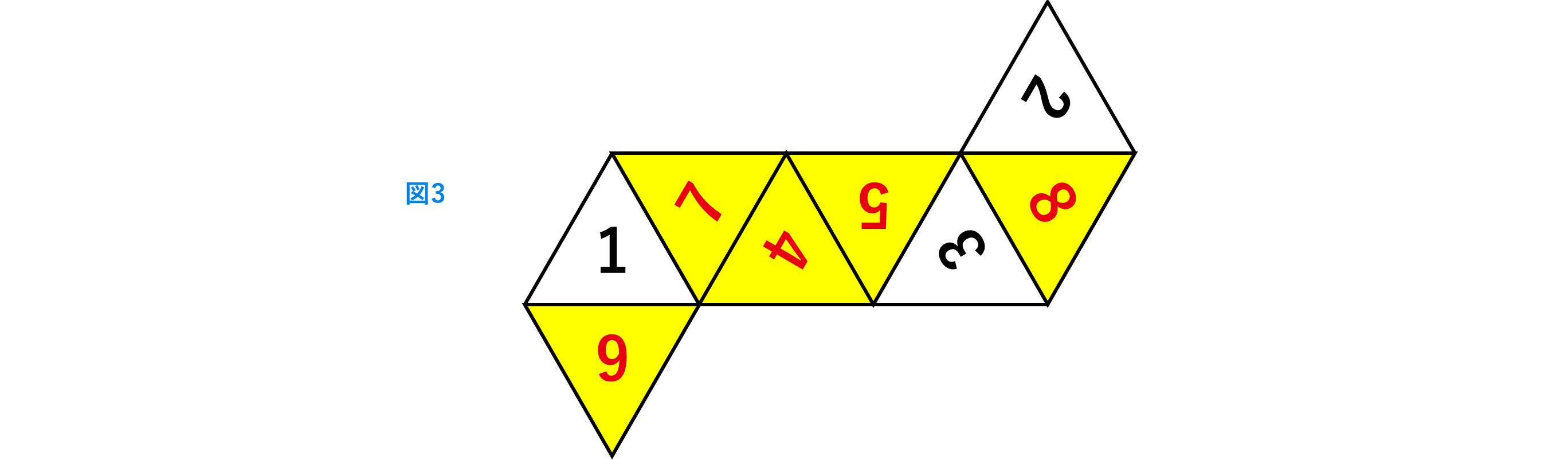
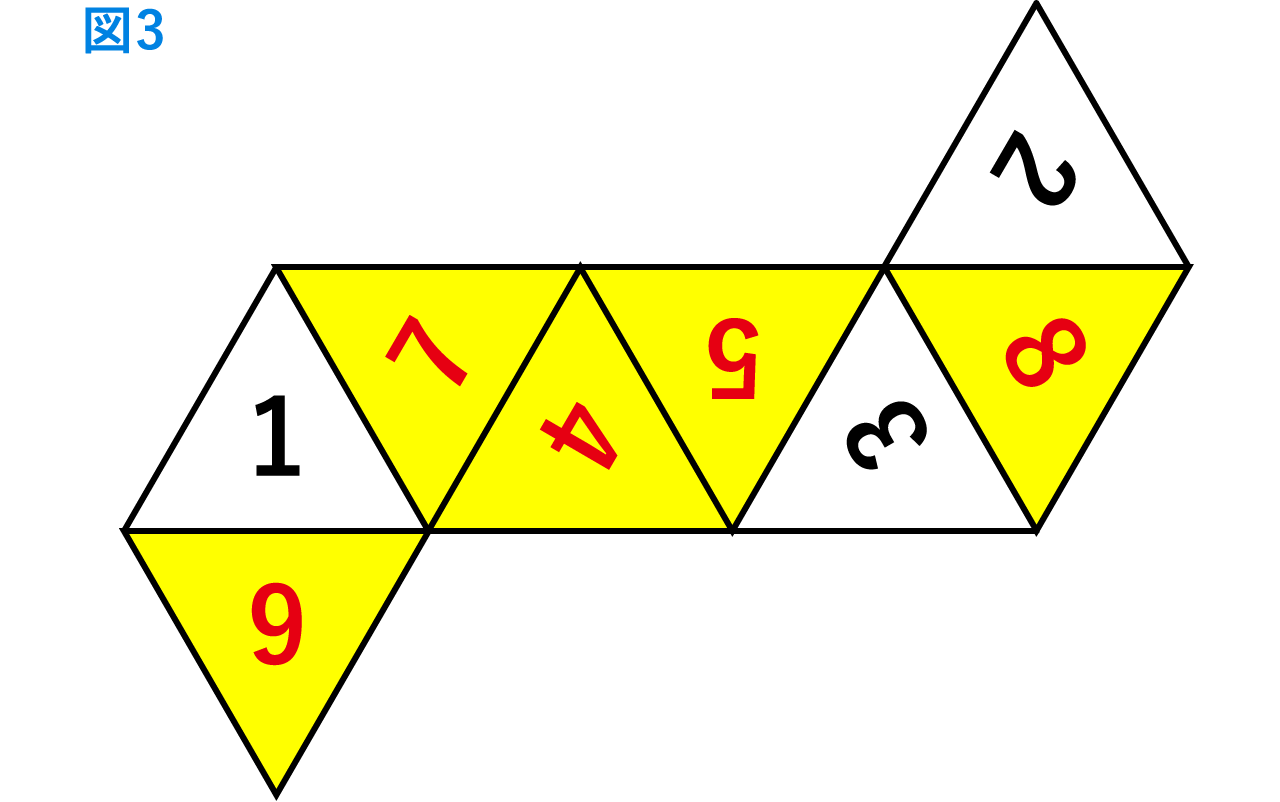
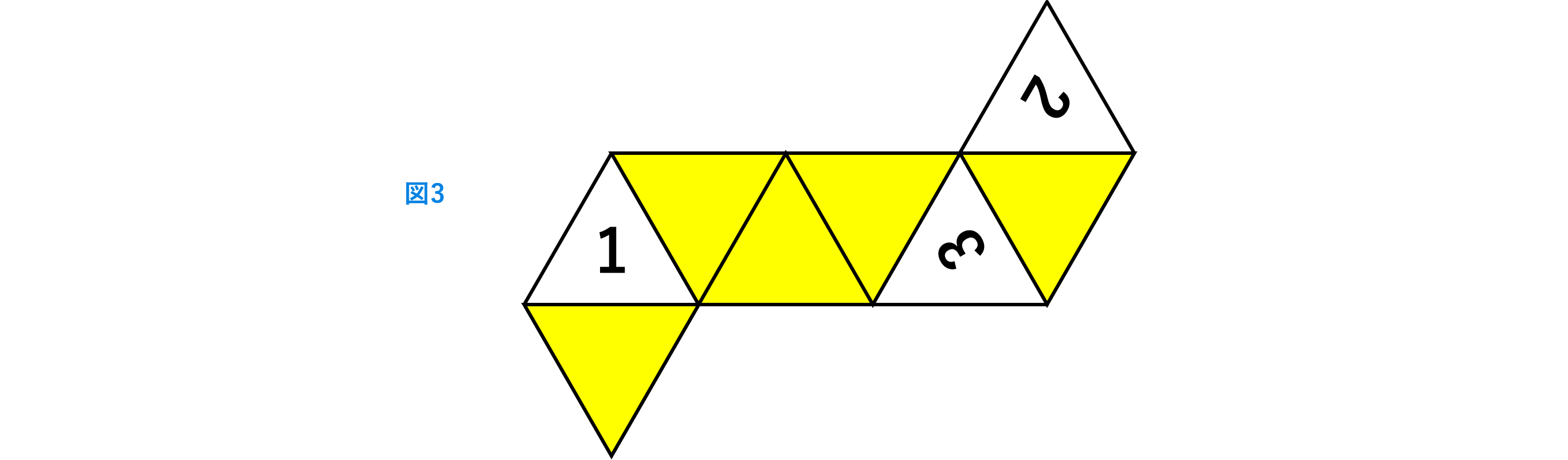
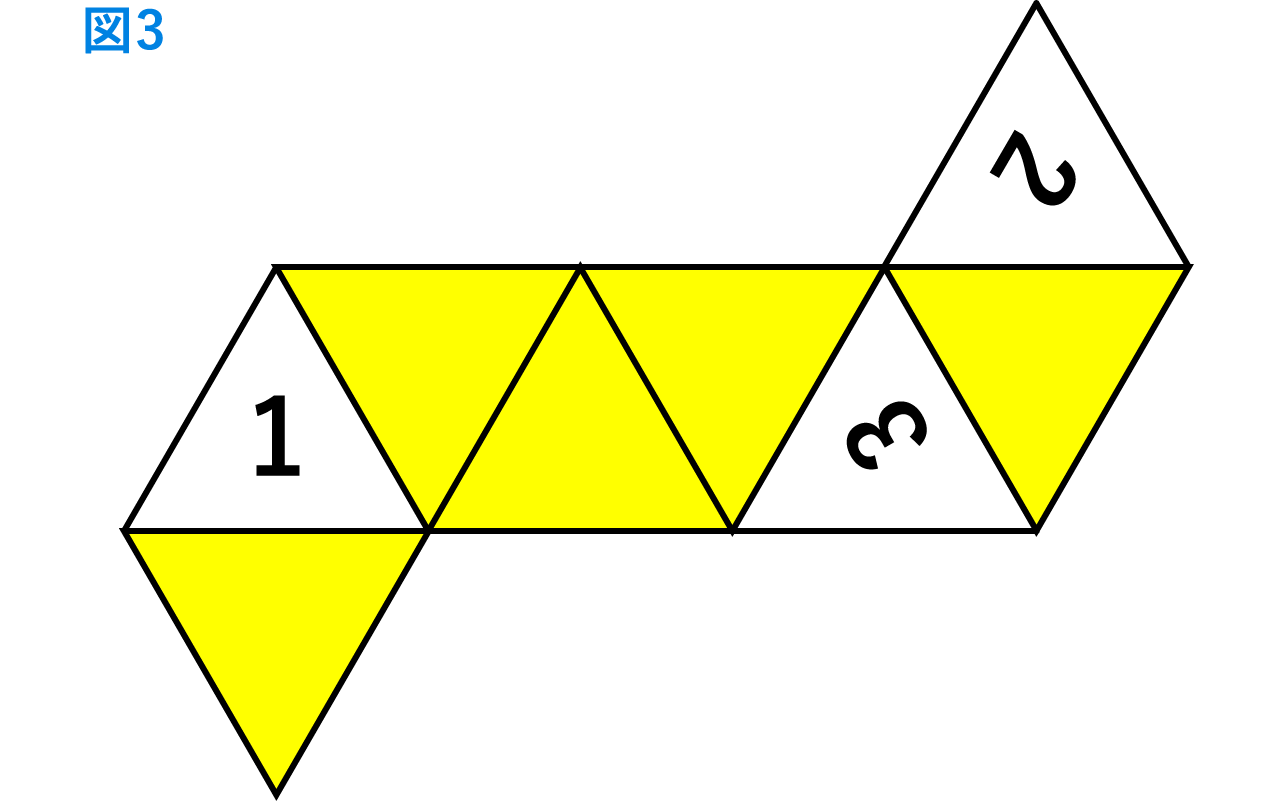
（４）この立体の展開図で、1，2，3の書かれている三角形の配置が図３のようになるとき、
他の数字を向きも正確に解答欄の展開図にかきこみなさい。